web3全栈体系
联系作者
联系作者

# 4.1 遍历链表节点

链表：在React中的Fiber中采用链表树的数据结构来解决主线程阻塞的问题，我们一起来试着遍历一个简单的链表结构试试

# 🍅 案例：遍历链表节点并对每个节点的value值求和

     // 链表
      const NodeD = {
          value: 4,
          next: null
        };

        const NodeC = {
          value: 3,
          next: NodeD
        };

        const NodeB = {
          value: 2,
          next: NodeC
        };

        const NodeA = {
          value: 1,
          next: NodeB
        };

        const LinkedList = {
          head: NodeA
        };

      // 以下是解题答案
      let num = 0;
      // 缓存函数
      let momoize=(func,hasher)=>{
          let cache ={}
          return function (...args) {
              let key= ""+(hasher?hasher.apply(this,args):args[0])
              if(!cache[key]){
                  cache[key]=func.apply(this,args)
              }
              return cache[key]  
          }
      }
      // 值相加函数
      let run =(linkedList, callback)=>{
          let head=linkedList.head
          while(head){
              callback(head.value)
              head=head.next
          }
          return num
      }

      var _momoize=momoize(run)

      function traversal(linkedList, callback) {
          _momoize(linkedList, callback)
      }

      // 调用2次，第二次会读取缓存函数
      traversal(LinkedList, current => (num += current));

      traversal(LinkedList, current => (num += current));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

# 4.2 Floyd判圈算法

含义： Floyd判圈算法(Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法(Tortoise and Hare Algorithm)，是一个可以在有限状态机、迭代函数或者 链表上判断是否存在环，求出该环的起点与长度的算法。 在图和树的数据结构在具体使用中，可能会出现循环依赖的情况，如何自动判断，是否存在循环，可以使用Floyd判圈算法

# 🍅 通俗讲解：Floyd判圈算法，这个其实就是在算法的设计中会设计快慢两个指针；也可以假设乌龟和兔子进行赛跑，如果他们相遇的话就代表环存在的，还因为这个像跑步比赛的过程中，那个跑的快的肯定会在跑环的时候反超那个跑得慢的人。

# 🍅 示例：

  1. 假设现在有两个指针，一个快指针和一个慢指针，然后快指针以2倍的速度推进，慢指针以1倍的速度推进；如果链表结构存在环形（就是循环依赖）的话，我们现在假设绿色是循环依赖的部分。
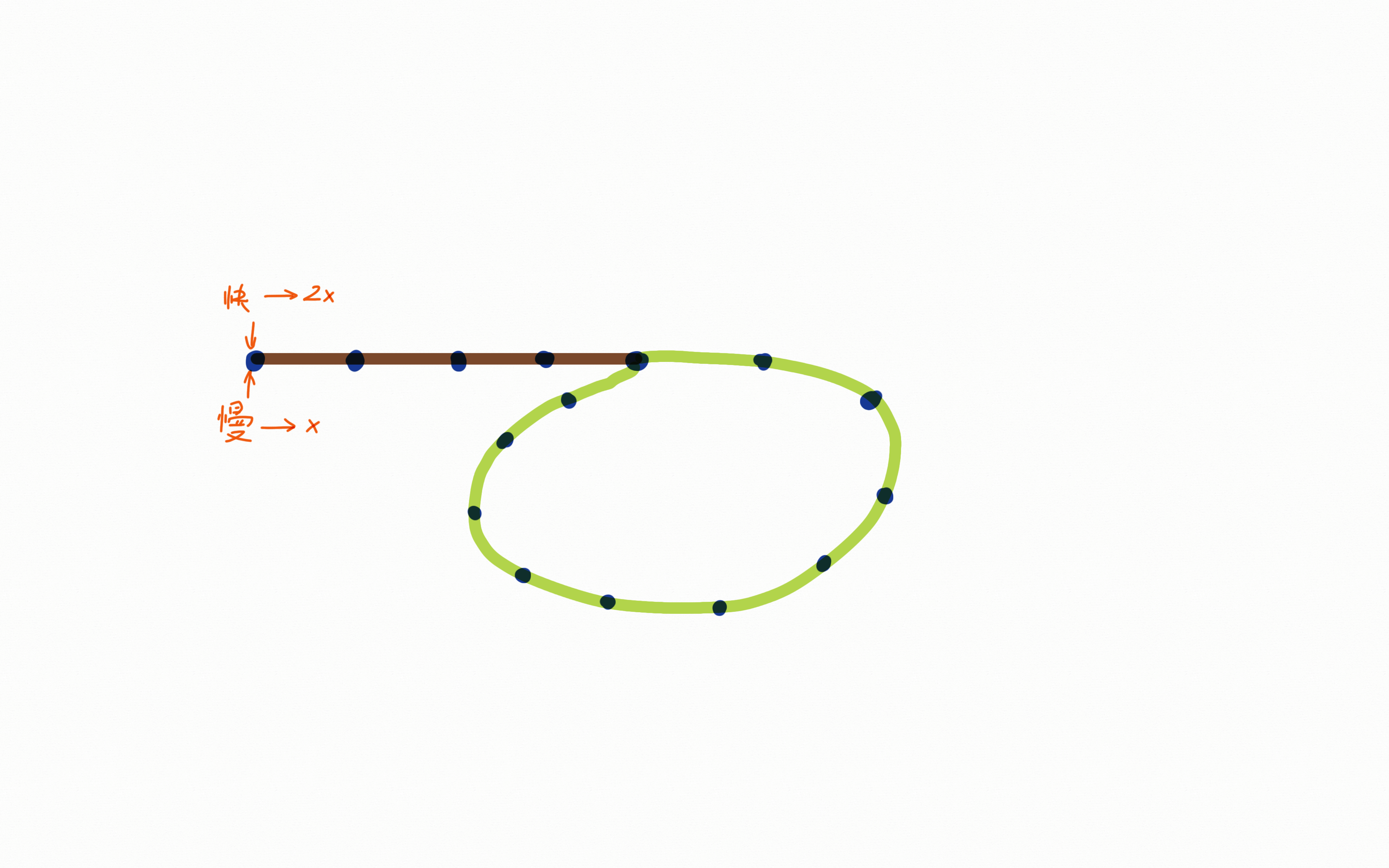
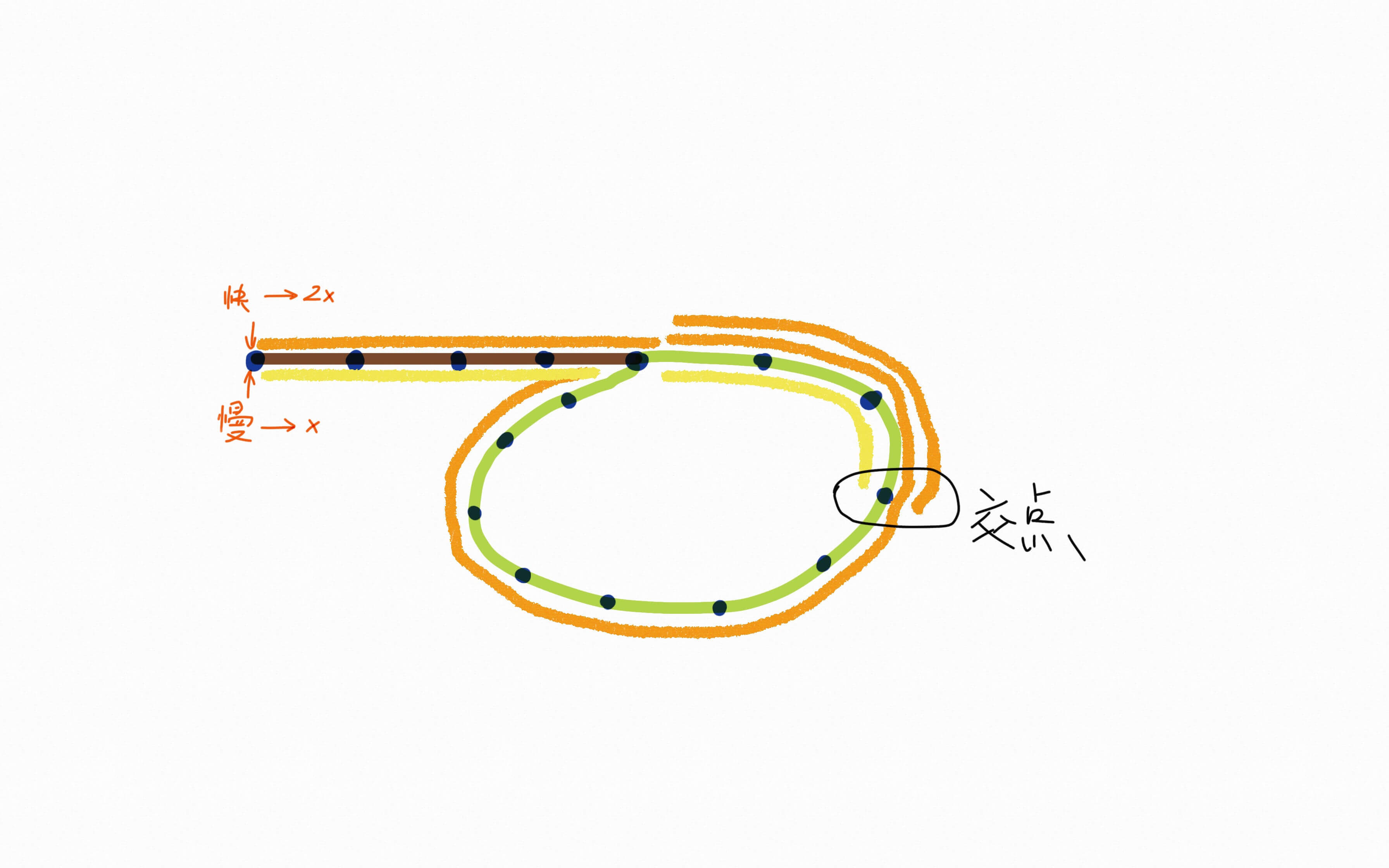
  2. 标交点的部分就是2个指针相遇的地方，在顺时针跑的过程中，橘黄色就是快指针移动的距离，黄色部分就是慢指针移动的距离，可以看出快指针比慢指针多跑了一圈，我们设计一个算法的话，其实要判断 是否有圈出现，就是判断快慢指针是否有重叠，也就是最后指向了同一个对象，那其实就是他们之间出现了循环依赖的过程。
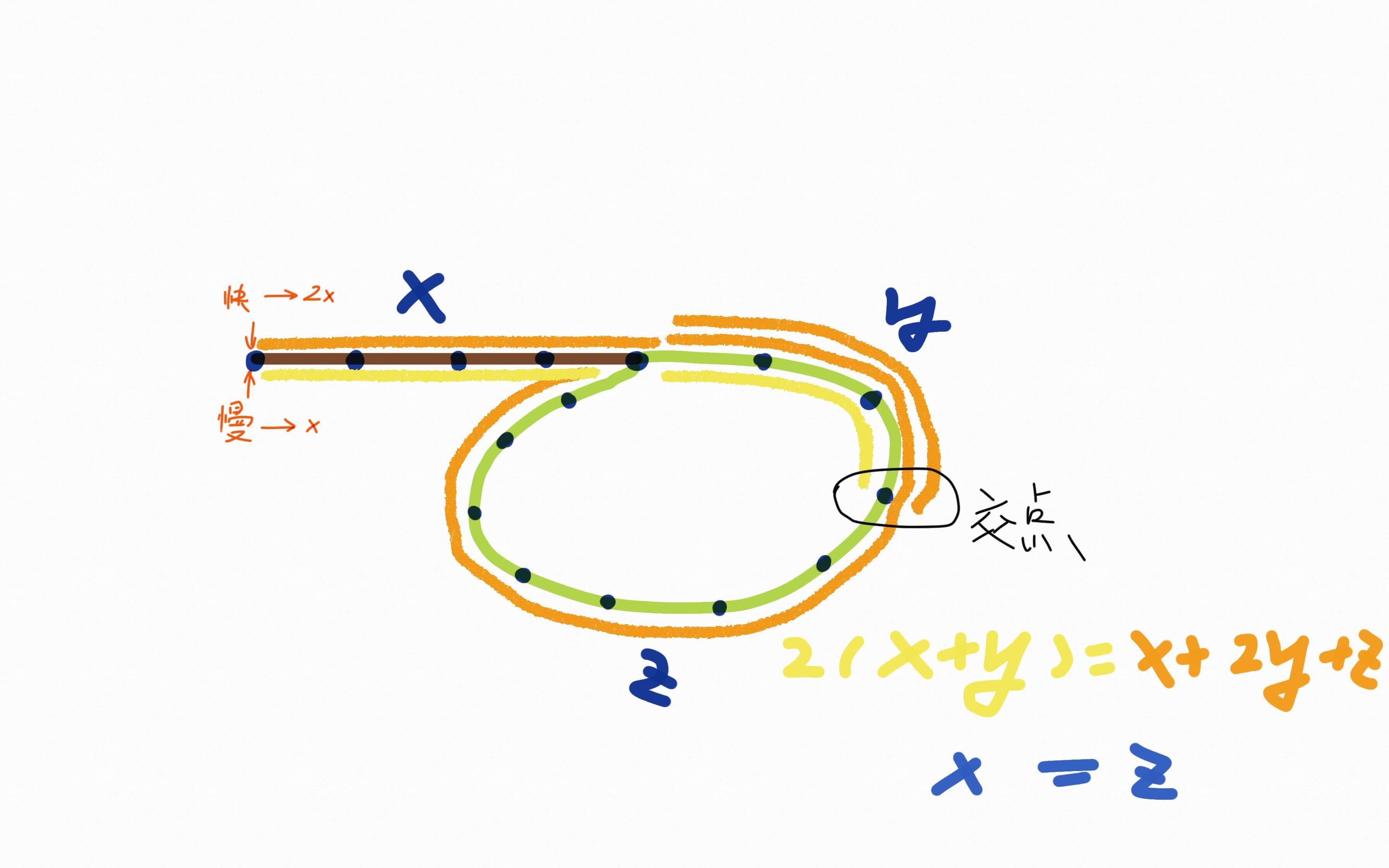
  3. 下图我们用x、y、z标识了3段距离，慢指针走的距离是x+y；快指针是x+2y+z，我们假设快指针的速度是慢指针的2倍；可以得出公式2(x+y)=x+2y+z，解题得出x=z，也就是说x的距离等于z的距离。

# 🍅 案例： 判断对象是否存在循环引用

     const c = {
        value: -4
      };

      const b = {
        value: 0
      };

      const a = {
        value: 2
      };

      const head = {
        value: 3
      };

      head.dep = a;
      a.dep = b;
      b.dep = c;
      c.dep = a;

      // 解答1，判断是否存在环
      const floyd1 = head => {
      try {
        let clone = JSON.parse(JSON.stringify(head));
        if (clone) return -1;
      } catch (err) {
        return 1;
      }
    };

  // 解答2 判断是否存在环,如果存在，环从哪开始
  const floyd2 = head => {

      //第一步判断是否有环
    let fast= head //快指针
    let slow= head //慢指针

    while(fast && fast.dep){
      fast=fast.dep.dep
      slow=slow.dep
      // 相等后，说明2者相遇了，说明存在循环
      if(fast===slow){
          break
      }
    }
    if(!fast || !fast.dep) return -1

  /**
  * 第二步判断环从哪开始,当快慢指针在交点相遇后，假设快指针是慢指针的2倍，
    快指针在往前走，同时一个指针从开始位置走
  * 他们相遇后，就是环开始的位置，可以参照图3，最后得出的x=z
  */
    let start=head
    let pos=0
    while(start!==fast){
      pos++
      start = start.dep
      fast = fast.dep
    }
    return pos
  };
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

# 4.3 字符串算法(最长公共子序列)

# 🍅 字符串算法？

在virtual DOM做Diff Patch操作中，有一条准则就是同一层的节点进行diff patch，从一个dom节点转换成另一个dom节点的过程我们可以 抽象的看成从字符串ABCDEGFG切换成ACDFG，如何保证在操作过程中尽量只做节点移动，减少插入和删除的操作是我们的目标。 简化来看就是要以最小的开销从ABCDEGFG切换成ACDFG。

# 🍅 什么是子序列？

一个字符串的子序列是指一个新的字符串，在不改变原序列相对位置的情况下删除原序列若干个元素（也可以不删除）之后得到的新序列，这个序列就原序列的子序列 例如：abcde的子序列有abcd、ace等，像aec不是该序列的子序列。

# 🍅 什么是最长公共子序列？（最长公共子序列简称lcs）

给定两个序列X和Y，这2个序列共同拥有最长的那个子序列，就是2个序列的最长公共子序列 例如：abbcbd和dbbceb最长公共子序列是bbcb。

应用场景：字符串相似度对比

# 🍅 参考文档：点击我 (opens new window)

# 🍅 案例： 求最长公共子序列

一般在解决算法的时候，一般有四种算法思想，分治法、动态规划、回溯法、贪心算法，这一题适合动态规划来做，因为这题符合动态规划的特点。

动态规划（英语：Dynamic programming，简称 DP）

动态规划的特点：

  1. 最优子结构：一个规模为n的问题可以转换成比他小的子问题来求解，最优解肯定是由最优的子解推导出来的
  2. 无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响
  3. 子问题重叠性：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到（并非必要性质）

最优子结构就比方说 "abcde" 和 "ace" 的最长公共子序列 因为俩个字符串最后的e都相同 那么他们的公共子序列 肯定是 “abcd”和 “ac” 的公共子序列数值上加1

其实动态规划的难点是归纳出递推式，在斐波那契数列中，递推式是已经给出的

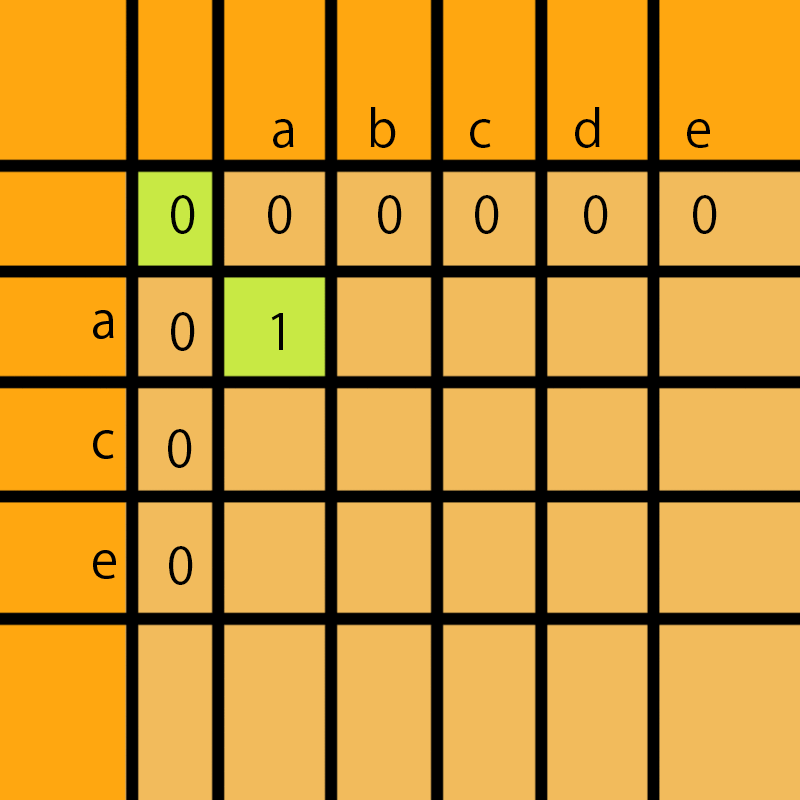
动态规划我们拿笔画一画，一个作为横轴一个作为纵轴，我们以2个字符串为例子，那么abcde作为横轴，ace作为纵轴，先初始化第一行和第一列；因为空字符串无论和 abcde 和 ace比，没有公共的子序列，所以都是0，在一个二维数组里存放的格式dp[[0,0,0,0,0],[0],[0]] 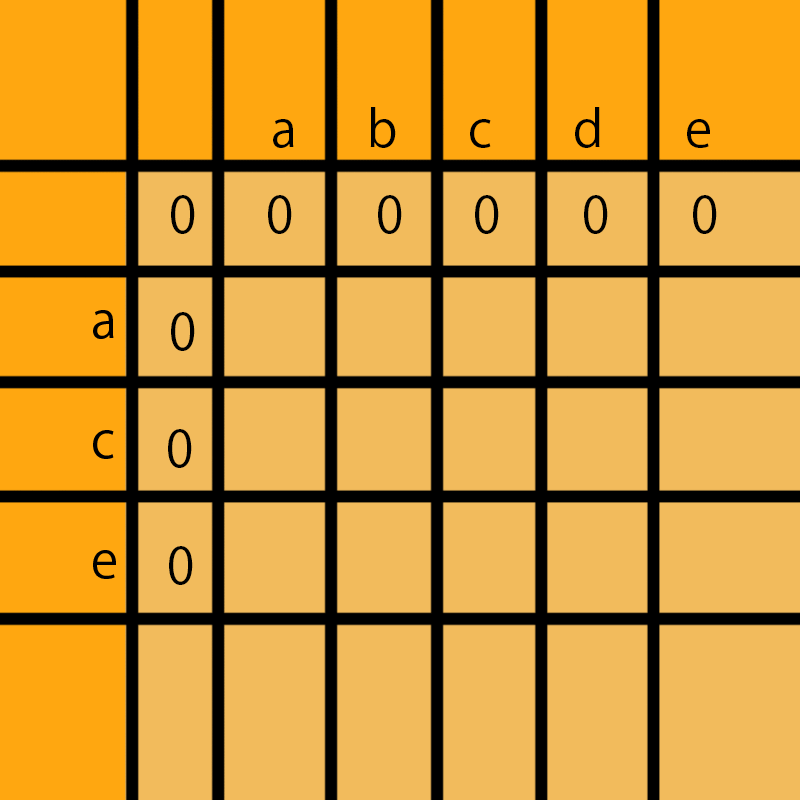a和a比有公共子序列a，那么这里就拿他们前面最优子解加上1，这个0加1等于1，所以这里填1。

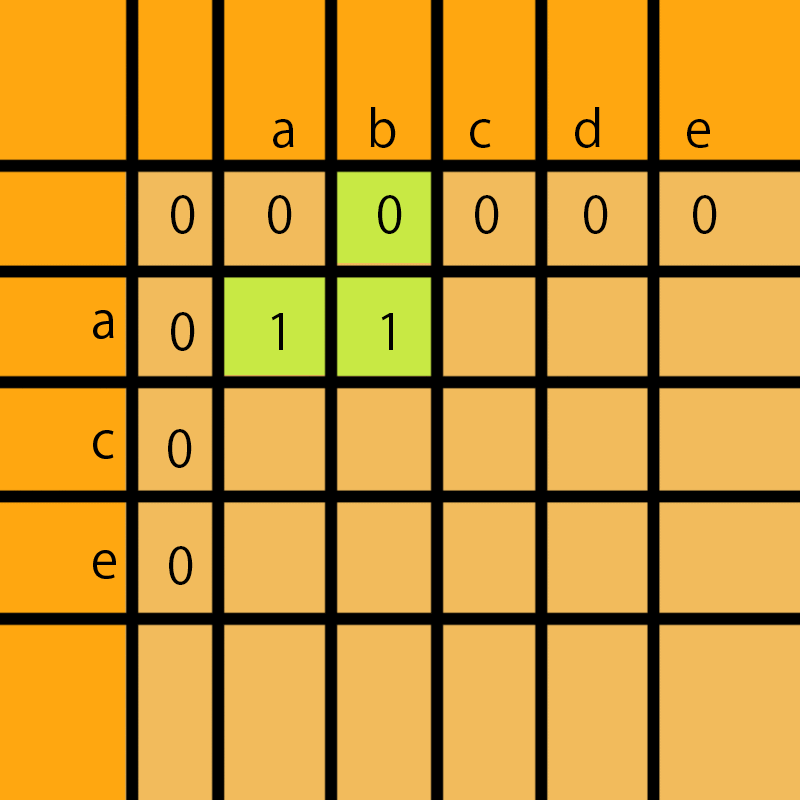
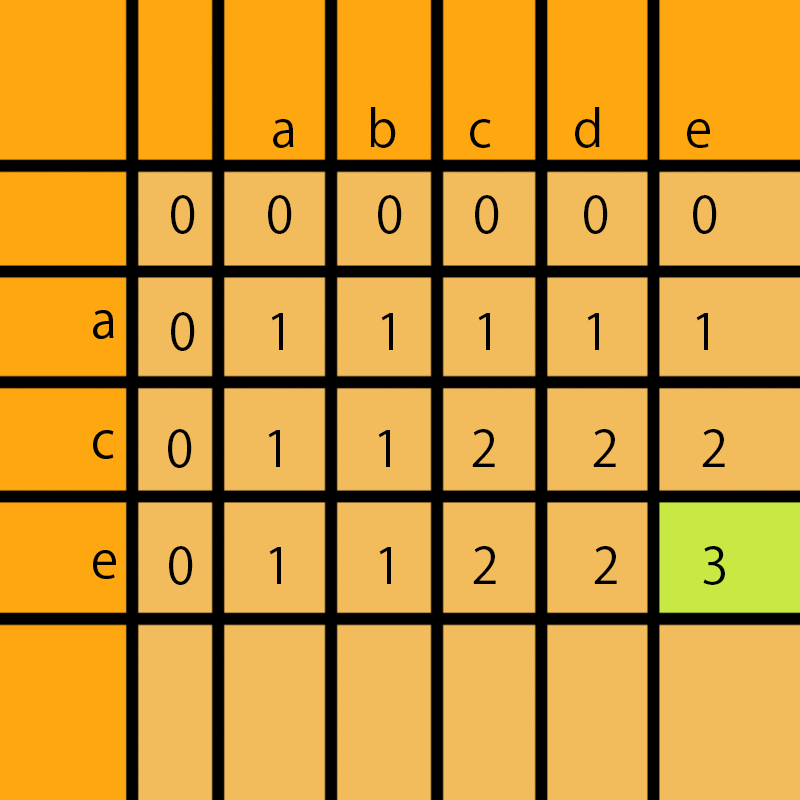
abcde的第i个字符和ace的第j个字符相等了，说明又多了一个相同的的字符，那么肯定拿他们前面的一个字符i-1和j-1的lcs上加1才是第i个字符和第j个字符的lcs a和b比不同，那么a和ab的公共子序列还是a；假如当前的a和ab的lcs的值存放再dp[i][j]中，那么我们要取dp[i-1][j]、dp[i][j-1]、dp[i-1][j-1]中最大的值存放在dp[i][j]中，dp[i-1][j-1]肯定是3个值最小值，所以可以忽略 a和bcde比没有公共部分，所以一直是1 我们存放在最后一行最后一列就是这2个字符串的最长的公共子序列

推导出公式

word1[i]==word2[j]: dp[i+1][j+1]=dp[i][j]+1

word1[i]!=word2[j]: dp[i+1][j+1]=Math.max(dp[i][j+1],dp[i+1][j])

    const lcsamples = {
      string1: "abcde",
      string2: "ace",
      count: 3
    }
  
  const longestCommonSubsequence = (word1,word2) => {
  var n=word1.length
  var m=word2.text1
  // 如果有一个空字符串，就返回0
  if(n*m===0){
    return 0
  }
  let dp=[(new Array(m+1)).fill(0)] //初始化第一行[[0, 0, 0, 0, 0, 0]]
   for(let i=0;i<n;i++){ //两个for循环遍历
     dp[i+1]=[0] //第一列
     for(let j=0;j<m;j++){
       // text1第i个字母和text2第j个字母相等了，在前面最优子结构上加1，就是现在的最长公共子序列，然后存在dp[i+1][j+1]的位置上
      if(word1[i]==word2[j]){
        dp[i+1][j+1]=dp[i][j]+1
      }else{
        dp[i+1][j+1]=Math.max(dp[i][j+1],dp[i+1][j])
      }
     }
   }
   return dp[dp.length-1][dp[0].length-1]   
  }
  const count=longestCommonSubsequence(lcsamples.string1,lcsamples.string1)
  console.log(count) //3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 4.4 莱温斯坦距离问题

含义：莱文斯坦距离，又称Levenshtein距离，是编辑距离的一种，指两个字串之间，由一个转成另一个所需最少编辑操作次数

# 🍅 参考文档：点击我 (opens new window)

# 🍅 案例：

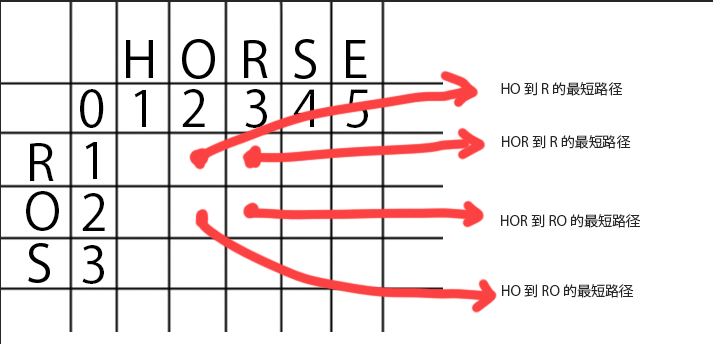
假设有2个字符串，第一行从空到s过程是增，E到空是删，E到s是改，这是编辑的3种情况 下图黑框代表任意的字符串，前面不管是什么，我们先比较最后一个，如果最后一个字符串不相等，在去比较前面的最优子结构加1，相等不加1，按照最优的子结构不断的迭代下去 最后一行最后一个字符相等情况，说明没有进行改变 计算两个单词horse和ros之间的编辑距离D，容易发现把单词变短会让问题变的简单，很自然利用D[n][m],表示单词长度n和m的编辑距离

具体来说D[i][j],表示horse前i个字母和ros的前j个字母的编辑距离

按照动态规划，横坐标是HORSE，纵坐标是ROS进行展开，第一行第一列是0，空字符串到空字符串不需要操作，所以是0，空字符串跟HORSE相比，不相同所以一直加1，空字符串到ROS相比不相同所以一直加1，这就是初始化了，下图我们可以看作一个棋盘

推导出公式 如果两个子串的最后一个字母相同的情况下 D[i][j]=(D[i−1][j−1]

否则我们将考虑替换最后一个字符使得他们相同 D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1]) 

// 莱文斯坦距离问题
const lsamples = [
   {
     string1: "horse",
     string2: "ros",
     count: 3
   },
   {
     string1: "intention",
     string2: "execution",
     count: 5
   }
 ];
//用一个二维数组d存储动态规划比较的值
 const Levenshtein = (word1, word2) => {
   var n=word1.length
   var m=word2.length
   let dp=[]
   // 如果有一个空字符串，就返回非空字符串长度
   if(n*m===0){
     return n+m
   }
   for(let i=0;i<n+1;i++){
     dp.push([])
     for(let j=0;j<m+1;j++){
       if(i===0){
         // 初始化第一行
         dp[i][j]=j
       }else if(j===0){
         // 初始化第一列
         dp[i][j]=i
       }else if(word1[i-1]===word2[j-1]){
         dp[i][j]=d[i-1][j-1]
       }else {
         dp[i][j]=Math.min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j])+1
       }
     }
   }
   console.log(d)
   return d[n][m]
 }

 lsamples.forEach(({string1,string2,count})=>{
     console.log(Levenshtein(string1,string2),count)

 })
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
最新更新时间: 2024/6/20 00:39:57

← 认识同构及原理 →

© 2024 web3全栈体系. All Rights Reserved.（所有文章未经授权禁止转载、摘编、复制或建立镜像，如有违反，追究法律责任。）

蜀ICP备20023457号-1